1. VAE 개념

AE(Auto Encoder) : 잠재 공간(Latent Variable)에 값을 저장한다.
잠재 공간에서는 input x에 대해 자신을 언제든지 reconstruct 할 수 있는 "z를 만드는 것"
VAE : 잠재 공간에 확률분포를 저장하므로, 평균과 분산 파라미터를 생성한다.
input x가 만들어지는 확률분포를 찾고, 다른 Data에 대해 이 확률분포(Variational Distribution)를 활용
주 목적은 Latent space(즉, 이미지의 특징)를 Decoder에 통과시켜 결과를 얻는 것
=> Decoder를 학습
그리고 여기서 Decoder를 학습시키기 위해 Encoder를 앞단에 붙여 특징을 뽑는 과정이 추가된다는 것이다.
2. VAE - Approximate Model
VAE의 궁극적인 목표는 Posterior distribution을 찾는 것이다.
이를 위해 Likelihood(모델에서 데이터 값이 나올 확률)와 사전확률이 필요하다.
L(distribution | data) : 입력 데이터는 고정되어있지만 분포는 변하는 상황
-> "데이터가 주어졌을때 분포가 데이터를 얼마나 잘 설명하는가"

그런데 VAE는 Interactable model로, 입력 Data들을 모두 만족시키는 실제 Model을 찾기 매우 어렵다.
이러한 어려움으로 인해 Model에서 데이터가 나올 확률 즉, Liklihood를 찾는 것도 매우 어려울 것이다.
그래서 Posterior Distribution과 "근사하는" Approximate Distribution을 만든다.
이 근사하는 분포를 학습해 결과적으로 Varitational Distribution을 찾게 되는 것이다.

>대강 설명하면 이런 과정을 따르게 되지만, 조금 더 자세히 설명해보겠다.
3. VAE Loss Function

VAE의 loss function은 사진과 같은 식을 나타낸다.
하지만 이를 증명하기 위해 우선 Kullback Leibler Divergence부터 파악해보자.
3-1. KL Divergence
Kullback Leibler Divergence는 쉽게 말해 두 확률 분포 간의 차이다.

결국 KL Divergence는, 두 확률 분포간의 차이가 가까워 질 수록 값이 작아지고, 두 확률 분포가 완전히 동일하게 된다면, KL Divergence 값은 0이 되기 때문에 KL Divergence값은 모두 0이상인 값을 갖는다.

3-2. MLE
: Maximum Likelihood Estimation
즉, MLE는 "최대가능도 추정법"으로 주어진 표본에 대해 가능도를 가장 크게 하는 모수 𝜃 를 찾는 방법이다.

위 그림에서 decoder만 보고 설명하자면, decoder output이 x일 확률이 pθ(x)가 된다는 것이고,
VAE를 통해 학습하려는 것이 결국 입력 데이터 x에 대한 확률 분포 P(x)가 되겠으며
이는 가지고 있는 데이터를 기반으로 주어진 데이터 x가 나올 가능성이 가장 큰 확률 분포를 찾는 것이다.
decoder output이 X일 확률 pθ(x)를 최대화하는 확률 분포를 갖는 것이 목표
그런데 우리는 P(x)를 바로 알 수가 없다.
그래서 이를 추정하기 위해 잠재변수 z의 조건부 확률 분포 P(z|x)와 P(x|z)를 사용해 P(x)를 근사화시키게 되는 것이다.

여기서
- : 잠재 변수 z가 주어졌을 때 데이터 x가 생성될 확률을 나타내는 우도(likelihood), 즉 디코더(decoder).
- : 잠재 변수 z의 사전 확률(prior).
이제 문제는 우리가 이 모델을 학습하고자 할 때, 우도를 직접 계산하는 것은 불가능하기 때문에 위 방법으로 계산이 불가능함. (**적분이 너무 복잡하여 계산 불가능(intractable)**)
pθ(x)를 구하기 위해 인코더와 디코더를 도입하여 근사 posterior를 학습하게 된다.

- data likelihood인 p(x)를 최대화시키도록
- 해당 log(p(x))는 단조 증가함수 log를 씌워주고 Expectation 형식으로 변형
(단, 조건으로 z의 분포가 x가 인코더를 거쳐서 나오는 확률 분포를 제시) - Baye's Rule로 인해 log 안에 값을 변형, 다음에 분모 분자에 같은 q_pi 값을 곱함
- 해당 expectation 식을 3개의 항으로 분리
- 두 번째 항과 세번째 항은 KL divergence의 꼴로 변형 가능
- 세 번째 항은 decoder에서의 x given z 확률을 알아야만 구할 수 있는 값
-> 그러나, 본래 decoder가 z given x의 상황을 생각해보면 구할수 없는 값임
(KL divergence로 부터 나오는 값이므로 0이상인 값이라는 것만 파악)

3-3. Regularization Error

Regularization loss 두 가지 가정이 들어가는데,
첫번째 가정은 Encoder를 통과해서 나오는 분포는 다변량 정규분포를 따르는 것
두번째 가정은 latent space z의 분포는 표준정규분포를 따르는 것
위와 같이 정규분포를 따른다는 가정에 따라 p(z)에 N(0,1)을 넣으면 Regularization: 과 같이 깔끔하게 수식으로 정리된다.


위에서 제시한 Reconstruction error : 를 다시 정리하면
두 번째 줄의 저 값을 위해 적분을 계산해야하는데, 그렇게 못하기 때문에 샘플링 기법을 통해 근사화
(한 번만 샘플링해서 나온 저 녹색값을 구하는 것)
그래서 log x given z를 전체 데이터셋에 대해서 취해주면,
디코더에서 사용되는 p의 확률분포가 베르누이 분포를 따른다고 가정을 했을 때, 단순히 확률의 곱으로 표현을 해줄 수 있고 로그의 성질에 따라 전체 값을 log의 summation으로 나타내줄 수 있다.
그리고, 베르누이 식으로 바꾼 후 log의 정리를 하면 최종적으로 cross entropy식으로 정리된다.
4. Pi가 Gaussian distribution을 따를 때

우리는 잠재 변수 공간에서의 잠재 변수의 분포를 베르누이가 아닌 가우시안으로 모델링할 수 있다.
여기서 Pθ는 디코더 네트워크가 생성하는 확률 분포이기 때문에
Decoder 네트워크는 잠재 변수 공간에서 가우시안 분포를 따르는 데이터를 생성하도록 훈련한다.
Squared error 계산은 가우시안의 가정하에 사용되며,
Decoder가 잠재 변수 공간에서 가우시안 분포를 따르는 데이터를 생성한다고 가정하면 실제 데이터와 재구성된 데이터 간의 차이를 평가하기 위해 보통 squared error를 사용한다.
-> 이것은 예측된 값과 실제 값 사이의 차이의 제곱을 취한 것(Reconstruction Loss)
Reparameterization Trick
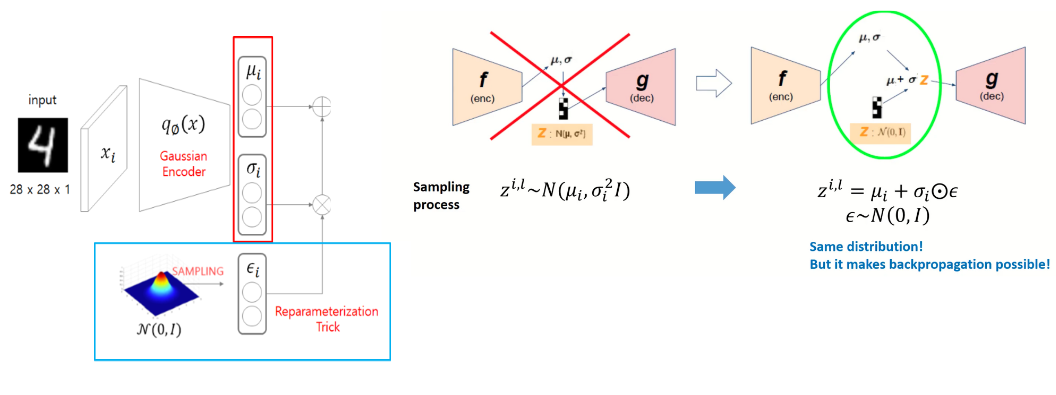
앞에서 자세히 설명하지 않아 이 부분에서 정리를 하겠다.
Reparameterization Trick은 학습 과정에서 필요한 샘플링과 역전파의 호환성을 확보하기 위한 기법이다.
VAE는 latent space에 데이터의 분포를 학습하고, 이 잠재 변수로부터 새로운 데이터를 생성할 수 있도록 학습한다.
잠재 공간의 변수 를 확률 분포로 정의하며, 일반적으로 정규 분포 를 사용한다는 것을 앞의 내용에서 공부했는데
문제는 VAE 학습 중에 샘플링 과정을 통해 잠재 변수 z를 얻는 부분에서 이 과정이 비결정적이므로 역전파로 모델 파라미터를 업데이트하기가 어렵다.
그래서 표준정규분포를 따르는 ϵ에 대해서 Encoder에서 나온 표준편차에 곱해주고
이를 다시 평균과 더해주는 연산을 취해준다면 미분을 할 수 있게 된다.
(샘플링 과정이 모델 파라미터 와 에 대한 결정적 함수가 되어 역전파를 통해 손실을 최소화하면서 학습 가능)
좌측에서는 Z가 정규 분포로 부터 샘플링을 한다는 정보만 있을 뿐 미분을 위한 식을 도출 할 수 없었는데,
우측에서는 표준 정규분포의 epsilon을 활용해 식을 만들어낼 수 있게 된다.

https://github.com/gmlfks/VAE_MNIST.git
GitHub - gmlfks/VAE_MNIST: VAE Image Generation using pytorch
VAE Image Generation using pytorch. Contribute to gmlfks/VAE_MNIST development by creating an account on GitHub.
github.com
'Deep Learning' 카테고리의 다른 글
| Cycle GAN (0) | 2024.10.11 |
|---|---|
| Conditional GAN (0) | 2024.10.11 |
| GAN (Generative Adversarial Network) (2) | 2024.03.24 |
| U-Net : Image segmentation | U-Net 구조 이해하기 (0) | 2024.02.04 |
| [Deep learning] Image Segmentation (2) | 2024.02.04 |
