https://www.acmicpc.net/problem/1753
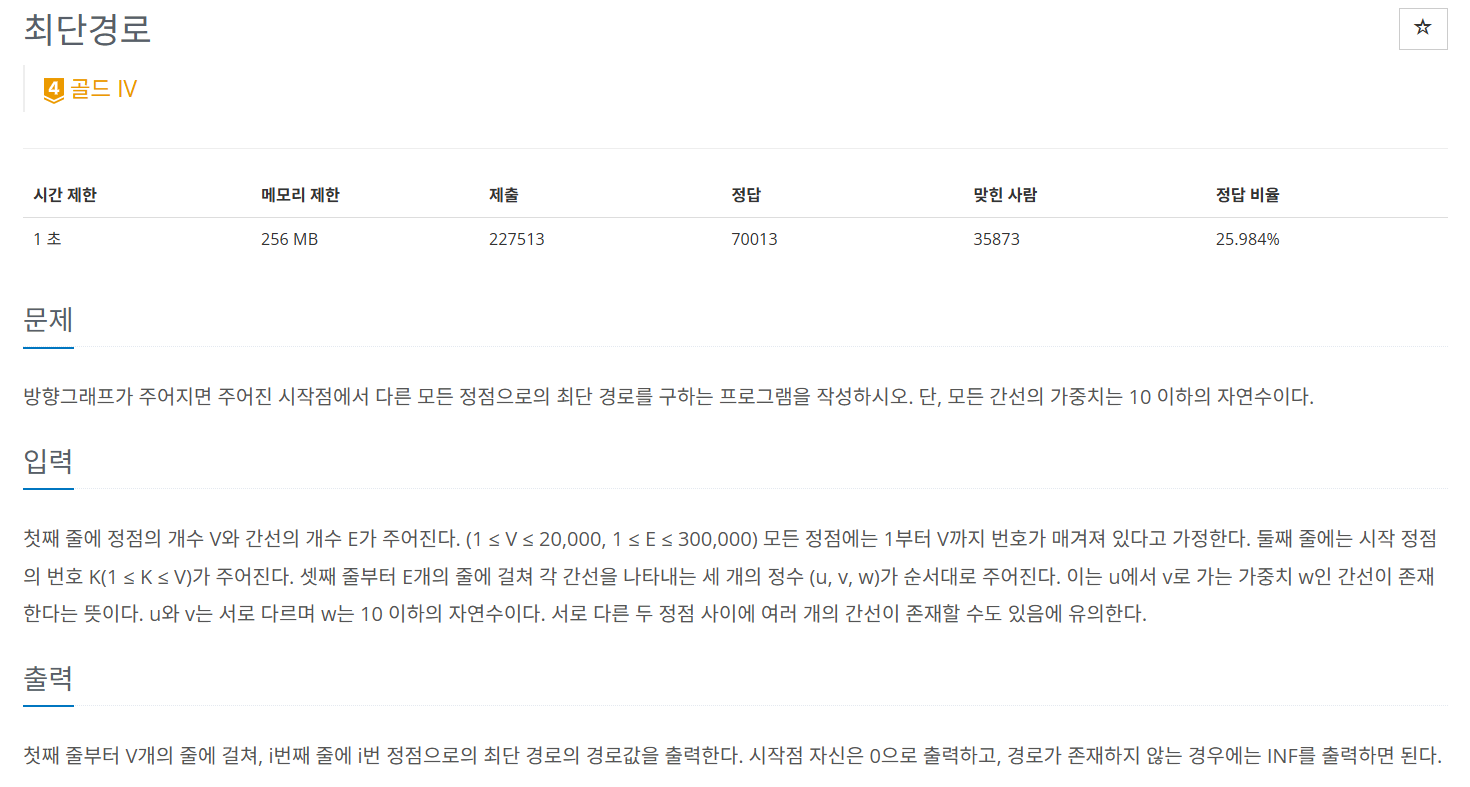
해당 백준 문제는 다익스트라 알고리즘을 사용한, 최단 경로를 구하는 문제이다.
우선, 다익스트라 알고리즘에 대해 설명해보도록 하겠다.
1. 다익스트라 알고리즘이란?
https://www.youtube.com/watch?v=pVfj6mxhdMw
첨부한 유튜브 영상을 통해 쉽게 이해할 수 있지만
다익스트라(Dijkstra) 알고리즘은 그래프에서 한 정점에서 다른 모든 정점으로의 최단 경로를 찾는 알고리즘이다.
이 알고리즘은 비음수 가중치를 가진 그래프에서만 사용할 수 있다.
- 방향 그래프 또는 무방향 그래프
- 각 간선에 대한 비음수 가중치
- 시작 정점
위 세가지가 주어지면, 시작 정점에서 모든 정점까지의 최단 거리를 구하면 된다.
여기서 간선 가중치는 반드시 0 이상이어야 하고, 음수 가중치가 있는 경우엔 벨만-포드 알고리즘을 사용해야 한다.
(다음 게시물에 설명)
다익스트라의 핵심 아이디어는
- 그리디 알고리즘 기반 : 현재 단계에서 가장 최적의 선택(가장 짧은 거리)을 하며 진행
- 현재까지 발견된 최단 경로를 확정짓고, 이를 이용해 다음 정점들의 최단 거리를 계산
- "우선순위 큐"를 사용하여 최소의 시간복잡도로 계산
2. 알고리즘 코드 설명
(1) 우선, Node를 표현하는 Edge클래스를 정의한다.
간선 정보를 저장하며, Comparable 인터페이스를 구현해 우선순위 큐에서 정렬 기준(가중치)을 설정한다.
이후 다익스트라 알고리즘 구현부에서 알게 되겠지만, 우선 순위 큐에서 poll()을 호출하면 항상 현재 큐에 있는 노드 중 우선순위가 가장 높은 노드(가중치가 가장 작은 노드)가 반환되어야 한다.
이 동작은 당연히 우선순위 큐의 내부 정렬 규칙에 의해 보장될 것이다.
static class Edge implements Comparable<Edge> {
int vertex;
int weight;
public Edge(int vertex, int weight) {
this.vertex = vertex;
this.weight = weight;
}
@Override
public int compareTo(Edge other) {
return this.weight - other.weight; // 오름차순 정렬
}
이때, 정렬 규칙이 Comparable 인터페이스의 compareTo 메서드를 기준으로 정렬되므로
Edge 클래스 내에 compareTo가 가중치를 기준으로 오름차순 정렬을 하도록 한다.
그럼, 가중치가 작은 순으로 우선 순위 큐에 들어가게 될 것이다.
this.weight가 other.weight보다 작다면, this가 우선순위 큐에서 먼저 나오게 되고, 반대의 경우는 other가 먼저 나온다.
(2) main 동작
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int V = sc.nextInt(); // 정점의 개수
int E = sc.nextInt(); // 간선의 개수
int K = sc.nextInt(); // 시작 정점
// 인접 리스트 생성
List<List<Edge>> graph = new ArrayList<>();
for (int i = 0; i <= V; i++) {
graph.add(new ArrayList<>());
}
// 간선 정보 입력
for (int i = 0; i < E; i++) {
int u = sc.nextInt();
int v = sc.nextInt();
int w = sc.nextInt();
graph.get(u).add(new Edge(v, w));
}
// 다익스트라 알고리즘 실행
int[] distances = dijkstra(V, K, graph);
// 결과 출력
for (int i = 1; i <= V; i++) {
if (distances[i] == Integer.MAX_VALUE) {
System.out.println("INF");
} else {
System.out.println(distances[i]);
}
}
}
이 부분은 다익스트라 알고리즘을 실행하기 전 정점과 간선, 시작 정점을 입력 받고
간선 정보를 입력한다.
distances[] 배열은 다익스트라 알고리즘 수행 후 각 정점까지의 최단 거리를 출력하는 부분이다.
distances[i] 즉, 정점 i까지의 최단 거리가 MAX_VALUE라는 것은 도달할 수 없는 정점을 의미한다.
(3) Dijkstra argorithm
앞서 말했듯이 우선 순위 큐를 정의하면 된다. 그 전에,
- distances 배열은 시작 정점에서 각 정점까지의 최단 거리를 저장한다.
- 처음에는 모든 정점까지의 거리를 무한대 (Integer.MAX_VALUE)로 설정, 이는 아직 어떤 경로도 발견되지 않았음을 의미
- 시작 정점(start)의 거리는 0으로 설정한다. 이는 자기 자신까지의 거리는 항상 0이기 때문
// 최단 거리 배열 초기화
int[] distances = new int[V + 1];
Arrays.fill(distances, Integer.MAX_VALUE);
distances[start] = 0;
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.add(new Edge(start, 0));
while (!pq.isEmpty()) {
Edge current = pq.poll();
int currentVertex = current.vertex;
int currentWeight = current.weight;
// 이미 처리된 경로라면 무시
if (currentWeight > distances[currentVertex]) {
continue;
}
// 현재 정점에서 연결된 간선 탐색
for (Edge edge : graph.get(currentVertex)) {
int nextVertex = edge.vertex;
int newDist = distances[currentVertex] + edge.weight;
// 더 짧은 경로를 발견하면 갱신
if (newDist < distances[nextVertex]) {
distances[nextVertex] = newDist;
pq.add(new Edge(nextVertex, newDist));
}
}
}
return distances;
그 다음 우선 순위 큐를 초기화한다. 큐는 현재까지 발견된 가장 짧은 경로를 기준으로 정렬된다. (compareTo)
처음에는 시작 정점만 큐에 add하고, 시작 정점의 거리는 0으로 설정한다.
- 우선순위 큐에서 가장 짧은 경로를 가진 정점(current)을 꺼낸다.
- current.vertex: 현재 처리 중인 정점 번호
- current.weight: 시작점에서 이 정점까지의 거리(최단 거리 후보)
currentWeight가 distances[currentVertex]보다 크다면, 이전에 더 짧은 경로로 해당 정점을 이미 처리했다는 뜻이다.
이 경우에는 현재 경로를 무시한다.
for (Edge edge : graph.get(currentVertex)) {
int nextVertex = edge.vertex;
int newDist = distances[currentVertex] + edge.weight;
이 부분에서는 현재 정점에서 연결된 모든 간선을 탐색한다.
- nextVertex: 연결된 정점
- edge.weight: 현재 정점에서 nextVertex까지의 가중치
- newDist: 시작 정점에서 nextVertex까지의 새로운 경로 거리
그리고 만약 탐색 중 더 짧은 경로를 발견하면 이를 갱신시키면 된다.
if (newDist < distances[nextVertex]) {
distances[nextVertex] = newDist;
pq.add(new Edge(nextVertex, newDist));
}
- newDist가 현재 기록된 최단 거리(distances[nextVertex])보다 작으면, 더 짧은 경로를 발견한 것
- 해당 정점(nextVertex)의 최단 거리를 갱신
- 갱신된 정점과 새로운 거리를 우선순위 큐에 추가하여 이후 탐색을 계속
3. Full code
처음 풀어보는 알고리즘이라면, 익숙해지는 데 많은 연습이 필요할 것 같다.
import java.util.*;
public class Main {
static class Edge implements Comparable<Edge> {
int vertex;
int weight;
public Edge(int vertex, int weight) {
this.vertex = vertex;
this.weight = weight;
}
@Override
public int compareTo(Edge other) {
return this.weight - other.weight; // 가중치를 기준으로 오름차순 정렬
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 입력 받기
int V = sc.nextInt(); // 정점의 개수
int E = sc.nextInt(); // 간선의 개수
int K = sc.nextInt(); // 시작 정점 번호
// 그래프 초기화 (인접 리스트)
List<List<Edge>> graph = new ArrayList<>();
for (int i = 0; i <= V; i++) {
graph.add(new ArrayList<>());
}
// 간선 정보 입력
for (int i = 0; i < E; i++) {
int u = sc.nextInt(); // 출발 정점
int v = sc.nextInt(); // 도착 정점
int w = sc.nextInt(); // 가중치
graph.get(u).add(new Edge(v, w));
}
// 최단 경로 계산
int[] distances = dijkstra(V, K, graph);
// 결과 출력
for (int i = 1; i <= V; i++) {
if (distances[i] == Integer.MAX_VALUE) {
System.out.println("INF");
} else {
System.out.println(distances[i]);
}
}
sc.close();
}
public static int[] dijkstra(int V, int start, List<List<Edge>> graph) {
// 최단 거리 배열 초기화
int[] distances = new int[V + 1];
Arrays.fill(distances, Integer.MAX_VALUE);
distances[start] = 0;
// 우선순위 큐 초기화
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.add(new Edge(start, 0));
while (!pq.isEmpty()) {
Edge current = pq.poll();
int currentVertex = current.vertex;
int currentWeight = current.weight;
// 이미 처리된 경로라면 무시
if (currentWeight > distances[currentVertex]) {
continue;
}
// 현재 정점에서 연결된 간선 탐색
for (Edge edge : graph.get(currentVertex)) {
int nextVertex = edge.vertex;
int newDist = distances[currentVertex] + edge.weight;
// 더 짧은 경로를 발견하면 갱신
if (newDist < distances[nextVertex]) {
distances[nextVertex] = newDist;
pq.add(new Edge(nextVertex, newDist));
}
}
}
return distances;
}
}
'백준 > Gold' 카테고리의 다른 글
| [Gold-3] 2206번 | BFS | 자바(Java) (0) | 2024.11.23 |
|---|---|
| [Gold-4] 1707번 | 이분 그래프 | BFS | 자바(Java) (1) | 2024.11.21 |
| [Gold-3] 17299번 | 스택 | 자바(Java) (0) | 2024.11.16 |
| [Gold-4] 2293번 | 동적계획법(DP) | 자바(Java) (1) | 2024.11.14 |
| [Gold-3] 11049번 | 동적계획법(DP) | 자바(Java) (0) | 2024.11.12 |