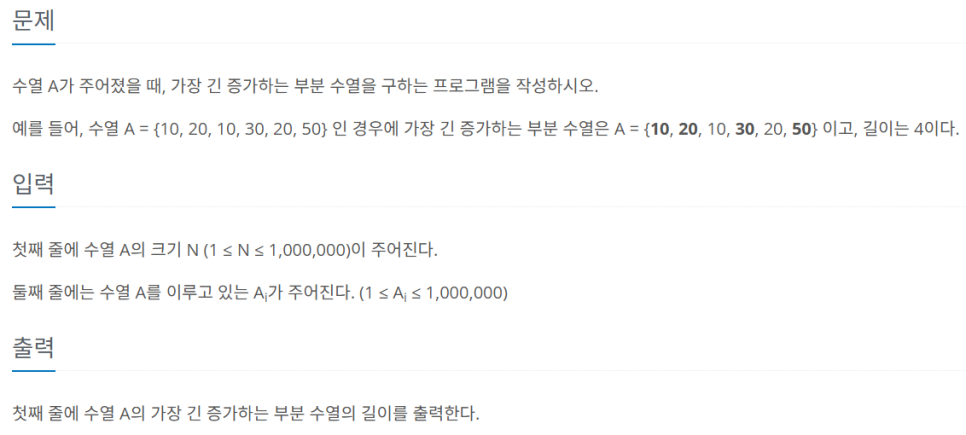
https://www.acmicpc.net/problem/12015
이분 탐색의 핵심은 *배열을 반씩 쪼개가며 찾기*이다.
그래서 배열 내에 특정 타겟값이 들어올 때, 왼쪽과 오른쪽은 이 타겟이 들어갈 위치를 찾기 위한 탐색 범위를 의미한다.
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 수열의 크기 입력
int N = Integer.parseInt(br.readLine());
int[] arr = new int[N];
// 수열 A 입력
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
// LIS 길이를 구하는 함수 호출
System.out.println(LIS(arr, N));
}우선 원소 수인 N 값과 배열 안의 값을 for문으로 입력 받은 후,
본격적으로 LIS 함수를 설명하면
public static int LIS(int[] arr, int N) {
// dp 배열: 가장 작은 끝값을 저장하는 배열
// dp[i]는 길이가 i+1인 LIS의 마지막 값을 저장
List<Integer> dp = new ArrayList<>();
// 각 원소에 대해 이분 탐색을 진행
for (int i = 0; i < N; i++) {
int target = arr[i];
// 이분 탐색을 통해 삽입할 위치를 찾음
int left = 0, right = dp.size();
while (left < right) {
int mid = (left + right) / 2;
if (dp.get(mid) < target) {
left = mid + 1;
} else {
right = mid;
}
}
// dp에 삽입할 위치가 left임
if (left == dp.size()) {
dp.add(target); // 새로운 LIS 끝값 추가
} else {
dp.set(left, target); // 기존 값을 대체
}
}
// dp 배열의 길이가 가장 긴 증가하는 부분 수열의 길이
return dp.size();
}1. left = 0, right = list.size():
- left는 탐색 범위의 시작 인덱스(0), right는 탐색 범위의 끝 인덱스를 나타냄
right는 `list.size()`로 설정되어 있기 때문에 "배열의 크기만큼" 탐색함
- left와 right의 범위 내에서 target이 들어갈 적절한 위치를 찾음
2. mid = (left + right) / 2:
- mid는 left와 right의 중간값. 이 값이 바로 현재 탐색 범위의 중간 위치로, 여기서 target과 비교하여 left와 right를 좁혀갈 것.
3. if (list.get(mid) < target):
- 만약 중간값 list.get(mid)가 target보다 작으면, target은 중간값보다 오른쪽에 있어야 하므로, left = mid + 1로 탐색 범위를 오른쪽으로 좁힘
4. else right = mid:
- 만약 중간값 list.get(mid)가 target보다 크거나 같으면, target은 중간값의 왼쪽에 있을 수 있으므로, right = mid로 탐색 범위를 왼쪽으로 좁힘
- 이때 target이 **중간값과 같을 경우**에도 right = mid가 되니까, 정확히 그 위치에 target을 삽입하거나 대체
### 예시
`target = 25`, `list = [10, 20, 30]`
- 초기 상태: left = 0, right = 3
- 1차: mid = (0 + 3) / 2 = 1, list.get(1) = 20
- list.get(1) < 25, 따라서 left = mid + 1 = 2
- 2차: mid = (2 + 3) / 2 = 2, list.get(2) = 30
- list.get(2) > 25, 따라서 right = mid = 2
- 종료: left == right == 2, target이 들어갈 위치는 인덱스 2
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 수열의 크기 입력
int N = Integer.parseInt(br.readLine());
int[] arr = new int[N];
// 수열 A 입력
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
// LIS 길이를 구하는 함수 호출
System.out.println(LIS(arr, N));
}
// LIS를 구하는 함수
public static int LIS(int[] arr, int N) {
// dp 배열: 가장 작은 끝값을 저장하는 배열
// dp[i]는 길이가 i+1인 LIS의 마지막 값을 저장
List<Integer> dp = new ArrayList<>();
// 각 원소에 대해 이분 탐색을 진행
for (int i = 0; i < N; i++) {
int target = arr[i];
// 이분 탐색을 통해 삽입할 위치를 찾음
int left = 0, right = dp.size();
while (left < right) {
int mid = (left + right) / 2;
if (dp.get(mid) < target) {
left = mid + 1;
} else {
right = mid;
}
}
// dp에 삽입할 위치가 left임
if (left == dp.size()) {
dp.add(target); // 새로운 LIS 끝값 추가
} else {
dp.set(left, target); // 기존 값을 대체
}
}
// dp 배열의 길이가 가장 긴 증가하는 부분 수열의 길이
return dp.size();
}
}'백준 > Gold' 카테고리의 다른 글
| [Gold-4] 1707번 | 이분 그래프 | BFS | 자바(Java) (1) | 2024.11.21 |
|---|---|
| [Gold-3] 17299번 | 스택 | 자바(Java) (0) | 2024.11.16 |
| [Gold-4] 2293번 | 동적계획법(DP) | 자바(Java) (1) | 2024.11.14 |
| [Gold-3] 11049번 | 동적계획법(DP) | 자바(Java) (0) | 2024.11.12 |
| [Gold-3] 11066번 | 동적계획법(DP) | 자바(Java) (0) | 2024.11.12 |