Feature extraction
오디오 데이터 특징 추출은 오디오 신호에서 유용한 정보를 추출하는 과정이다.
오디오 데이터 자체가 무겁고 복잡하기 때문에 주요 특징들을 추출하여 데이터를 다루게 된다.
(고차원성, 데이터 분석, 차원 감소, 일반화 등등)
그리고 이러한 오디오 데이터 특징 추출의 가장 대표적인 기법이 MFCC(Mel-Frequency cepstral coefficients)이다.

MFCC(Mel-Frequency Cepstral Conefficient)
Audio 신호 처리에 쓰이는 특징값(Feature)

MFCC는 다음과 같은 과정으로 일어난다.
1. 프레임 분할(Frame Segmentation) :
오디오 신호를 일정 시간 간격의 작은 프레임으로 분할
-> 시간에 따른 변화를 추적 (20ms~50ms의 프레임 크기 사용)
프레임 길이는 오디오 신호의 주파수 해상도와 시간 해상도 사이의 균형을 유지하는 중요한 요소이다.
2. 프레임에 대한 윈도우 함수 적용(Windowing) :
각각의 프레임에 대해 윈도우 함수를 적용시켜 시간 영역에서의 불연속성을 줄인다.
프레임간의 부드러운 전환을 유지하고, 주파수 분석을 정확하게 수행할 수 있다.
MFCC의 다음 단계들을 보기 전,
Windowing에 대해 자세히 살펴보겠다.
Windowing
푸리에 변환을 위해 시간 프레임으로 잘라서 처리하는 과정이다.
오디오 데이터는 0으로 시작해서 0으로 끝나야 한다.
프레임 분할 과정을 거치면서 파형이 끊어지거나 이어지지 않고 끝나게 된다.
이를 "불연속성" 이라고 한다.
불연속성은 주파수 스펙트럼에서 Noise처럼 동작하며, 이 노이즈 현상을 Spectral Leackage라고 한다.
이러한 불연속성을 줄이기 위해 윈도우 함수가 사용되어 프레임의 시작과 끝 부분을 부드럽게 만들어준다.

위 사진은 Hanning 윈도우 함수를 사용한 것이다.
윈도우 함수의 종류는 매우 많은데 주로 Hanning window를 사용한다.
1) 윈도우 함수 선택 : Hamming, Hanning, Blackman-Tukey 등
2) 윈도우 함수 생성 : 시간 축에 대해 일련의 값을 가지는 배열로 표현
3) 프레임에 윈도우 함수 적용 : 각각의 프레임에 해당하는 시간 영역에서 윈도우 함수의 값을 추출,
일반적으로 프레임 길이와 윈도우 함수의 길이가 같아야 한다.
윈도우 함수는 다음에 더 심층적으로 공부해야겠다,,~
3. 푸리에 변환(Fourier Transform) :
각 프레임에 대해 푸리에 변환을 적용하여 주파수 영역으로 변환한다.
-> 각 프레임에서의 주파수 성분 분석
푸리에 변환에 대해 자세히 알아보자.
Fourier Transform(푸리에 변환)
Audio 신호는 여러 주파수들의 결합으로 이루어 있어, waveform에서 특징을 추출하기 어렵다.
그래서, 푸리에 변환을 통해 waveform을 time-domain에서 frequency-domain으로 변환시킨다.
푸리에 변환은 연속 푸리에 변환 또는 이산 푸리에 변환을 사용한다.
이 둘은 신호가 연속적인지 이산적인지에 따라 다르다.
연속 푸리에 변환(Continous Fourier Transform) : 연속적인 시간 도메인의 신호에 대한 푸리에 변환
이산 푸리에 변환(Descrete Fourier Transform) : 이산 시간 도메인의 신호에 대한 푸리에 변환
그리고 MFCC에서는 FFT(Fast Fourier Transform)을 활용한다.
FFT : 디지털 신호 처리에서 주파수 도메인 분석을 위해 사용되는 알고리즘으로,
DFT를 효율적으로 계산하는 방법이다.
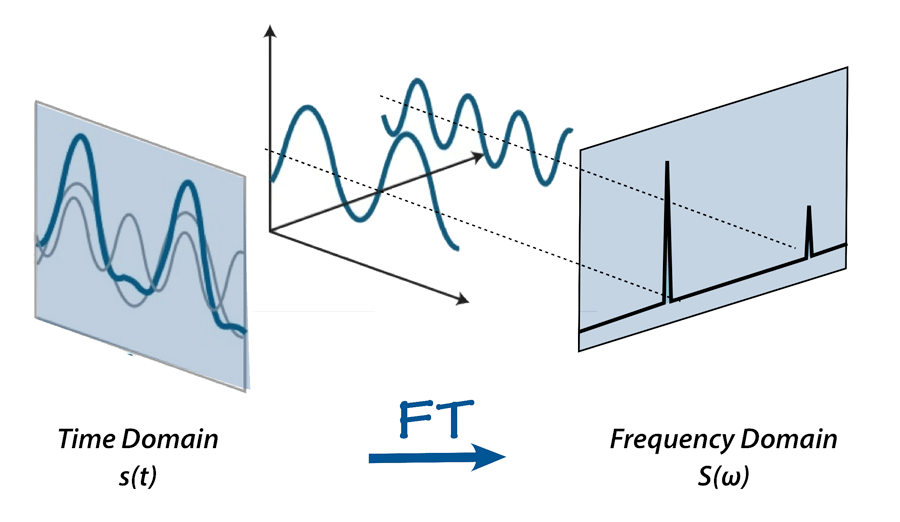
time-domain의 waveform을 fequency-domain으로 변환하여 신호가 어떤 주파수 성분을 포함하고 있는지 나타낸다.
신호를 여러 주파수 성분으로 분해하여 각 주파수의 진폭과 위상을 계산한다.
x축이 time에서 frequency -> Spectrum (주파수 영역에서의 신호의 표현)
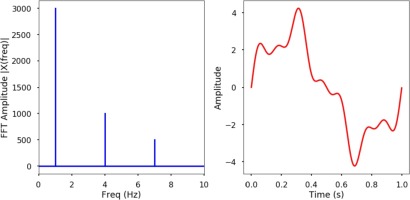
그리고, y축의 magnitude 제곱한 값을 power라고 하며 Power Spectrum을 표현할 수 있다.
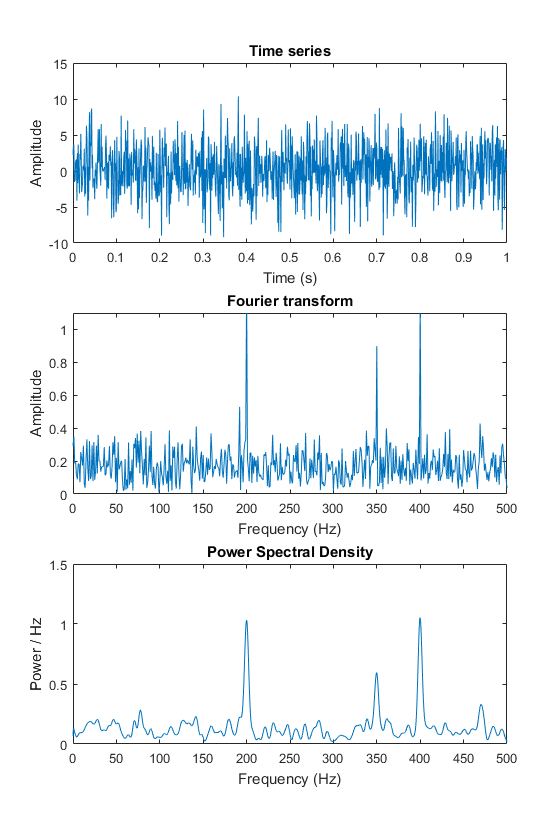
Spectrum은 일반적으로 주파수에 따른 진폭(amplitude)을 나타내며, 주파수 영역에서의 신호의 크기나 강도를 시각적으로 표현한다.
주로 선형 단위나 dB로 표현된다.
Power Spectrum은 주파수에 따른 파워(에너지)를 나타낸다. 이는 해당 주파수 성분이 전체 신호의 에너지에 어떤 비중을 차지하는지를 나타낸다. (강도를 파악하겠다는 뜻)
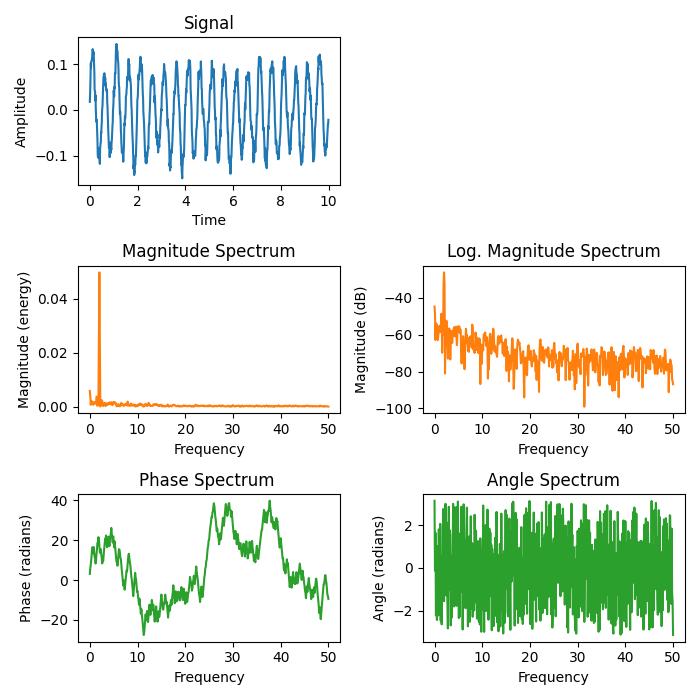
Log-Specturm은 주파수 영역에서의 신호를 로그 스케일로 표현한 것이다. 일반적으로 다양한 주파수 대역에서 크기가 다르게 나타나는데, 이를 선형 스케일로 표현하면 주파수 간의 상대적인 차이가 너무 크게 나타나기 때문에 log를 활용하게 된다.
그리고 데시벨(dB)는 신호의 강도나 에너지를 로그 스케일로 표현하는 데 사용되는 단위이다.
데시벨은 magnitude를 log 스케일링하여 구해진다.
데시벨(dB) =
푸리에 변환을 수행하고 나면 time-domain에 대한 정보가 사라지게 된다.
위에서 본 spectrum, power spectrum, log spectrum 모두 주파수 도메인에서의 신호 표현이며, 시간적 정보에 대해서는 직직접적으로 포함하지 않는다.
이러한 스펙트럼들을 시간 도메인에서의 정보를 포함한 분석을 위해 spectrogram을 사용해야한다.
자른 frame마다 푸리에 변환을 적용해 각각을 시간 순으로 쌓으면 time domain을 살릴 수 있다.
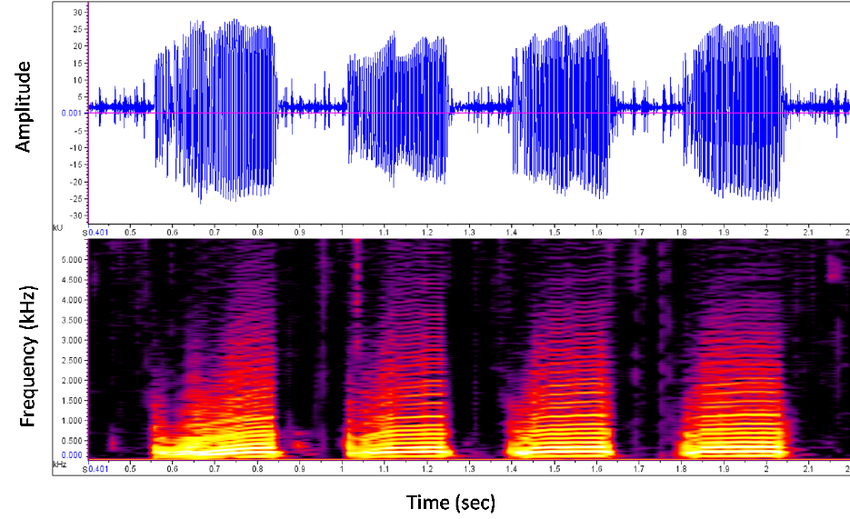
Spectrogram은 주파수와 시간에 대한 정보를 함께 시각화할 수 있다.
주로 파워 스펙트럼 또는 로그 스펙트럼을 기반으로 생성된다.
1. 시간 영역을 나누기 : 입력 신호를 시간적인 창(window)로 나눈다.
이 창은 프레임을 나타내며, 오버랩(overlap)이 있는 윈도우 함수를 사용한다.
2. 윈도우 함수 적용 : 프레임에 윈도우 함수를 적용하여 신호를 조작한다.
3. FFT : 각 윈도우마다 FFT를 수행하여 주파수 영역에서의 신호를 얻는다.
이를 통해 각 윈도우에서의 주파수 성분을 추출할 수 있다.
4. 파워 스펙트럼 또는 로그 스펙트럼 계산 : FFT 결과를 바탕으로 스펙트럼 또는 로그 스펙트럼을 계산한다.
5. 시각화 : 계산된 파워 스펙트럼이나 로그 스펙트럼을 세로로 세워 frame마다 쌓으면 푸리에 변환으로 사라졌던 time domain을 복원할 수 있다. 이를 spectrogram이라고 한다.
위 그림을 해석하면, x축이 time, y축이 frequency, 데시벨(dB)이 색으로 표현된다.
푸리에 변환을 통해 스펙트럼을 얻게 되었다.
이 다음, Mel spectrum 및 Log, DCT 과정에 대해 알아보자.
'Audio' 카테고리의 다른 글
| [Audio processing] Audio data feature 추출 이해하기 (2) (0) | 2024.02.10 |
|---|---|
| [Audio processing] Audio data 이해하기 (0) | 2024.02.09 |
